Softbody Phsyics Based Rodents

The Ultimate Ratformer Link to heading

What if we could physically simulate accurate rat physics, if rats had a tendency to balloon themselves in outsized proportions and also not act like rats at all?

Those familiar with Feynman and his revolutionary work will recognize this theoretical question he posed in his seminal lectures on physics.

Today it is finally answered.

Inspired by the physics of Jelly Car, I sought to replicate this, but in 3D.

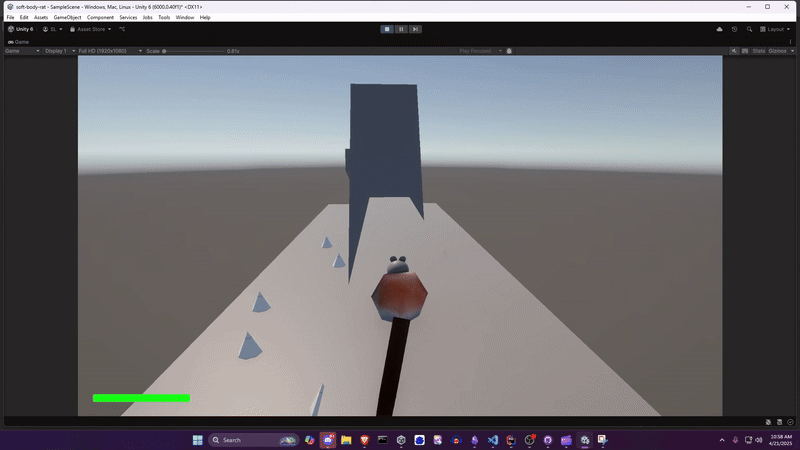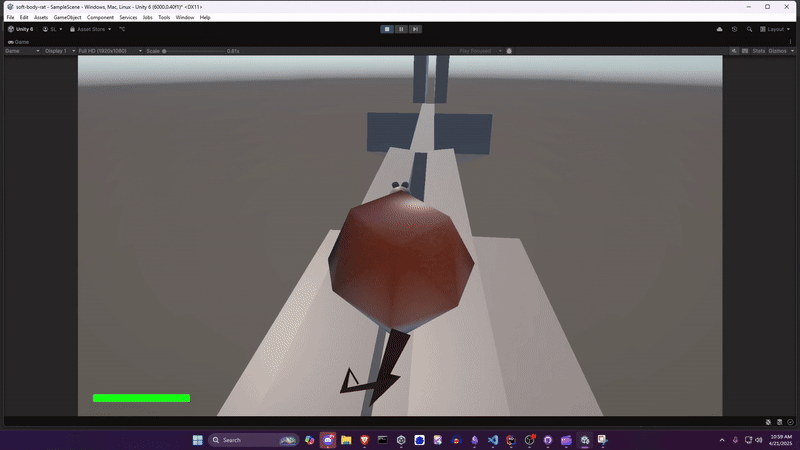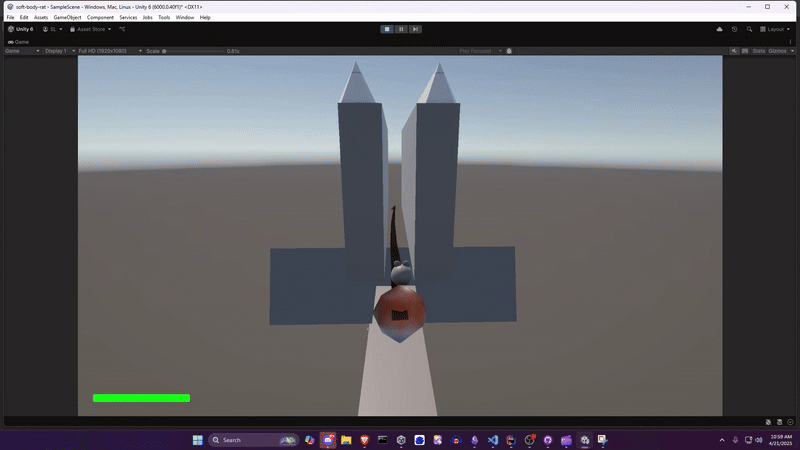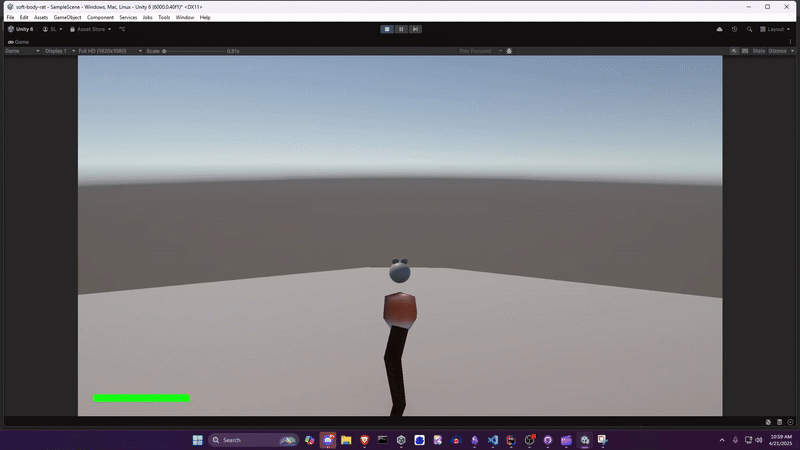
Initial Approach Link to heading

Initially I just built a blob. But players need something to connect to: a compelling character. And thus Ratformer (a platformer with rats) was conceived. While playing around with the blob, I felt it needed a tail, both to convey forward velocity, and because tail physics are fun to look at. And, well, if it has a tail, it needs a head.

Phsyics Breakdown Link to heading

• 16 points, arranged in a sphere, make up the body
• Each point has 18 forces acting on it at any given time:
  • 15 spring forces seeking to maintain a constant distance between each of the other points
  • 1 spring force “pushing” the point back to it’s original position, relative to the other 15 points
    • This is done to maintain the shape when all the points are on the same plane, which would cause the 15 spring forces to all push/pull along the same plane
  • 1 gravity force, pulling all the points down. This helps give the shape a “squishy” appearance when landing
  • 1 “pressure” force that push all points away from the computed center.
    • This also acts as the jump force, since lower points will push against the ground when “inflated”
• A Quickhull algorithm implementation that draws a mesh using the points as vertices

The points that make up the rat body

The body with the tail points

There’s many ways to skin a rat. This is the Quickhull method.

All in all, this feels very nice, even with limited tuning. This was a very iterative process; simply relying on baked in Unity physics is not enough for a nice feeling physically “accurate” game.

Iterative Designs Link to heading

Forces Link to heading

Each point initially only had spring forces between other points. This worked well enough, until large downward forces squashed all the points to a single plane, in which case no upward/downward force between the points was occuring, resulting in a soupy mess. I added a spring force to push it back to it’s theoretical “correct” position relative to the other points, which ended up being the exact force neccessary to push the points up from a “squashed” position

Gravity Link to heading

Constant gravity resulted in awkward movements. A common trick platformers use is to increase gravity during “falls”. This makes the character feel more reponsive and sticky. While not physically accurate, it gives a nice “punchy” feel to the jumps, and makes the player feel like they have more response time on the upward swing of the jump.

Even more unconstant gravity! Balloons afford a certain behaviour: floating. While they do in theory fall at the same rate literally everything else does, air resistance very obviously pushes up on the balloon, causing it to appear to fall slower. Well balloon rats happen to be the same. It felt weird the ballooned rat was falling at the same speed as the unballooned rat. The solution? Reduce gravity when ballooned. This gives it a nice floaty feel, and lets the player better control their fall when they unballoon.

Rotation Link to heading

First I tried rotating all the points so their forward direction aligned with the camera; a rat needs to be able to turn after all right? I quickly realized turning 16 rigidbodies in unision around a central point was somewhat outside of the scope of Unity physics; too many uncontrollable behaviours were popping up.

That’s where the head and tail come in. The body, being a sphere, doesn’t need to turn, we just need the player to think they’re turning. And what better way to convey that than to turn the head and tail?

Both the head and tail start point are simple spheres, constantly set at the point furthest from the camera on a circle projected from above onto the body of the rat. The implementation is simple yet elegant:

• Approximate a circle based on rat points in the same plane (X/Z plane)
• Find the average radius of the circle
• Place the head point (or tail point) at the point in the circle furthest from the camera, at the average radius distance. Do this once per frame and you have a head that moves on a “rail” around the rat, always facing the direction the camera is!

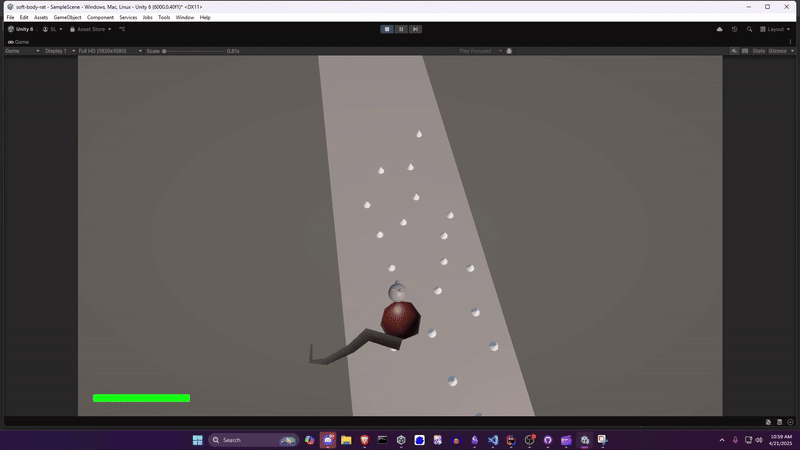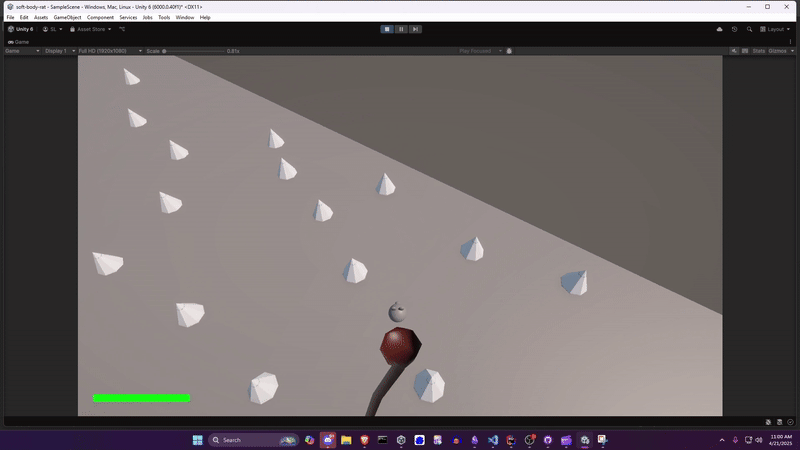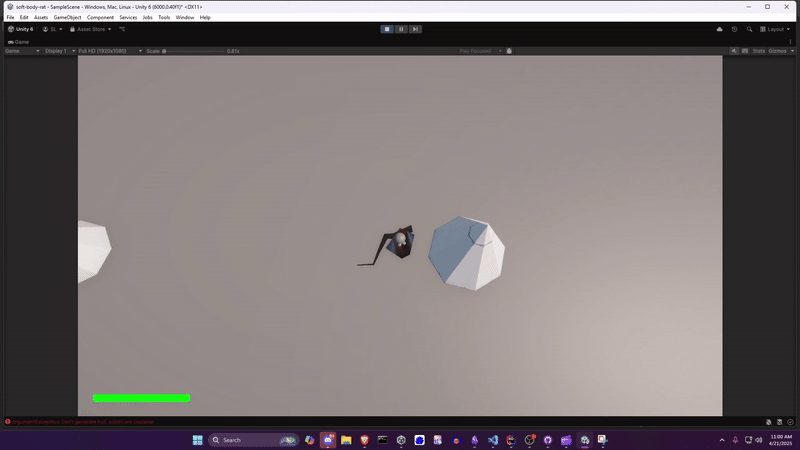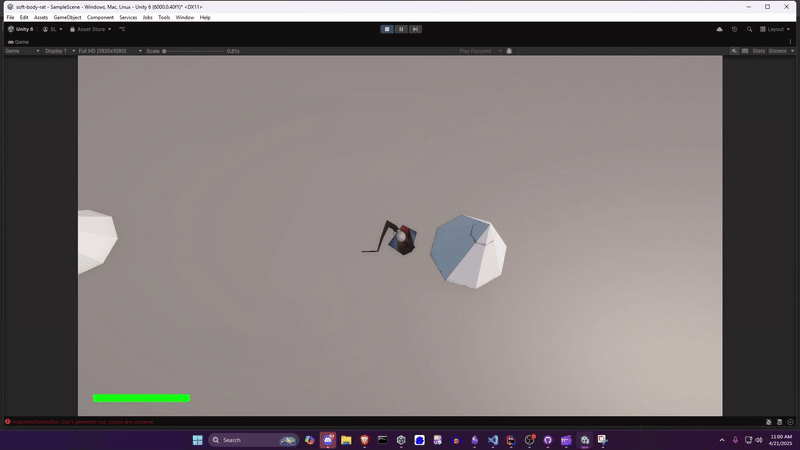
A bonus rat splat